等额支付系列的终值、现值、资金回收和偿债基金计算
二、等额支付系列的终值、现值、资金回收和偿债基金计算
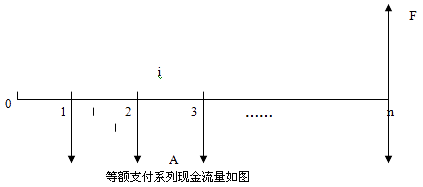
A 年金,发生在 ( 或折算为 ) 某一特定时间序列各计息期末(不包括零期) 的等额资金序列的价值。
1. 终值计算 ( 已知 A, 求 F)
等额支付系列现金流量的终值为 :
![]()
[(1+i)n-1]/i年称为等额支付系列终值系数或年金终值系数 , 用符号(F/A,i,n)表示。
公式又可写成:F=A(F/A,i,n)
例:若 10 年内,每年末存 1000 元,年利率 8%, 问 10 年末本利和为多少 ?
解 : 由公式得:
![]()
=1000×[(1+8%)10-1]/8%
=14487
2. 偿债基金计算 ( 已知 F, 求 A)
偿债基金计算式为:
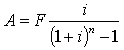
i/ [(1+i)n-1]称为等额支付系列偿债基金系数,用符号(A /F,i,n)表示。
则公式又可写成:A=F(A /F,i,n)
例:欲在 5 年终了时获得 10000 元,若每年存款金额相等,年利率为10%, 则每年末需存款多少 ?
解 : 由公式 (1Z101013-16) 得 :
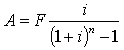
=10000×10%/ [(1+10%)5-1]
=1638 元
3. 现值计算 ( 已知 A, 求 P)
![]()
[(1+i)n-1]/i(1+i)n 称为等额支付系列现值系数或年金现值系数 , 用符号(P/A,i,n)表示。
公式又可写成: P=A(P/A,i,n)
例:如期望 5 年内每年未收回 1000 元,问在利率为 10% 时,开始需一次投资多少 ?
解 : 由公式得 :
![]()
=1000×[(1+10%)5-1]/10%(1+10%)5
=3790. 8 元
4. 资金回收计算 ( 已知 P, 求 A)
资金回收计算式为 :
![]()
i(1+i)n / [(1+i)n-1]称为等额支付系列资金回收系数,用符号(A/P,i,n)表示。
则公式又可写成:A=P(A/P,i,n)
例:若投资10000元,每年收回率为 8%, 在10年内收回全部本利,则每年应收回多少 ?
解 : 由公式得 :
![]()
=10000×8%×(1+8%)10/ [(1+8%)10-1]
=1490. 3 元
例.(2005真题)某施工企业现在对外投资200万元,5年后一次性收回本金和利息,若年基准收益率为8%,则总计可以收回资金( D )万元。
已知:(F/P,8%,5)=1.4693 (F/A,8%,5)=5.8666
(A/P,8%,5)=0.2505
A.234.66 B.250.50 C.280.00 D.293.86